Organizing Knowledge Through Knowledge Management

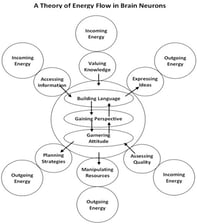
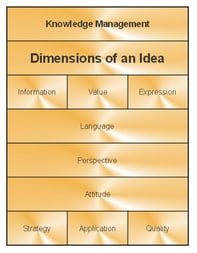
Understanding the relationship between the way we organize knowledge in each area of our personal knowledge systems, and the way we develop our motivations, is the second step in taking charge of learning. Each area of knowledge in our personal knowledge systems has a general structure. That structure is also reflected in the natural learning process. Our brains use the natural learning process to organize knowledge in a meaningful way.
Take the example of mathematics, which many find difficult to learn because they are not motivated. If we compare to another area of knowledge like playing a particular game or sport, we find it much easier to get motivated and to learn. This is because when our brains organize experiences according to the natural learning process, it is inherently motivational. Mathematics is usually approached as an academic subject and our brains have to learn it without the natural structure. When the brain is trying to learn out of context, the learning process becomes very tedious and difficult.
If we work at it long enough, our brains, which are extremely adaptive, will create artificial organizational structures associated with the material being learned and the motivation becomes the diploma or certificate we achieve for doing it. Although we may be able to achieve academic success in this way, we may never be able to use the knowledge for any practical purposes. If we ever try and use it in the real world, our brain has to reorganize it all over again according to the natural learning process. That is when we realize what the learning was all about. The difficulties that are encountered in teaching and learning mathematics is due to focusing on the mathematical structures and ignoring natural learning structures.
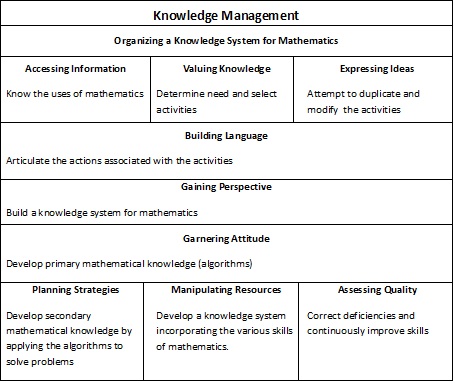
We can teach and learn mathematics more easily if we create real context. The knowledge management diagram shows how we can organize a knowledge system for mathematics. Building this knowledge system starts with knowing the uses of the mathematics we are going to learn. Our motivations start by establishing needs for the mathematics and identifying activities to achieve those needs. Establishing need is an essential part of learning. We have to duplicate and modify the activities to suit our needs and we have to articulate what we are doing using mathematical terminology.
Motivation requires being aware that we are building a knowledge system. That means that we are developing a general perspective of mathematics from the top down as our maturity develops and our knowledge increases. Motivation also requires that we are aware of the organizational structure we are building. We are not always conscious of building the structure but we are intuitively aware that it is happening. Intuition, which is the awareness of subconscious organizational activity, is the essence of motivation.
To build confidence and motivation in mathematics, we must know how to use numbers, add them, subtract them, multiply them, etc. to address our needs. This is primary mathematical knowledge and has to come from practical experience. As we use primary mathematical knowledge to solve problems, we develop secondary knowledge about the different ways we can use the primary knowledge. It is also important for as many of the problems as possible to be hands-on, especially in the initial knowledge building process. We need to measure and record actual objects and processes and show how mathematics is used to analyze properties and situations. And of course we need to continuously employ the general skills of estimating and correcting deficiencies as we learn.
This organizational approach can be applied to any area of knowledge we may have or aspire to develop. All knowledge systems will have primary and secondary knowledge. If we are learning mathematics and we use the example of pace in running to develop an understanding of division of numbers. The division is primary knowledge and the running is secondary. But if we are learning to run and we use division of numbers to calculate pace, then the running is primary knowledge and the division is secondary. There is a lot of overlap and interconnectivity in human knowledge and we can use knowledge from one area of our knowledge system to motivate learning in another.
In my next article, I will describe how to create useful knowledge systems by integrating primary and secondary knowledge to build meaningful learning projects.
Author Perspective: Business